
压力、体积、摩尔数和温度
在泄漏测试期间,测试部件的压力变化是主要关注点,当测试部件充满空气(或任何其他气体)时,它最初会在部件内部膨胀以占据其体积,当零件最终达到测试压力时,内部空气收缩。空气的这种快速膨胀和收缩会改变其温度和体积,由于温度和空气体积的变化,测试部分的温度和体积也会发生轻微变化。
为了检测泄漏,必须考虑压力的变化,压力的变化可能是由于温度、体积和气体摩尔数的变化而发生的。由于该过程涉及压力、体积和空气量等参数,因此受理想气体定律的支配。在数学上,该定律表示为:

P=容器内封闭的空气(或气体)的压力
V = 气体占用的容器体积
n= 气体的摩尔数
T = 气体的绝对温度
R = 理想气体常数,值为 0.0821 dm3atm K-1 mol-1
根据公式(1),任何数量的理想气体的压力和体积的乘积等于摩尔数、理想气体常数和气体绝对温度的乘积。从公式(1)可以看出,压力、温度和体积的变化是相关的,任何单个参数的变化都会影响其他参数。
根据气体的动力学分子理论(KMT),温度与给定气体样品的平均动能成正比。这可以表示为:

等式(1)涉及气体的实际实验行为,而等式(2)涉及使用KMT的实验分析结果。通过研究方程(1)和(2),我们可以看到在泄漏测试过程中压力,温度和体积是如何相互关联的。这意味着在泄漏测试期间,温度、测试部件体积和气体摩尔数的变化会影响部件的压力。
温度变化对测试部件压力的影响
当空气温度升高时,颗粒的平均动能和速度增加。这在上面的等式(2)中表示。这些粒子现在具有更大的速度,并且它们以更大的力撞击零件的壁。这些颗粒施加的压力本质上是每单位面积对零件壁施加的力。因此,压力随着温度的升高而增加。当容器的体积和气体摩尔数恒定时,压力与温度直接相关。
体积变化对测试部件压力的影响
当测试部件加压时,部件的壁会膨胀。这会导致零件体积发生变化。当零件膨胀且体积增加时,内部压力下降。发生这种情况是因为体积的增加增加了墙壁的面积。因此,单位面积的力(压力)下降,因为力是恒定的。在恒定温度下,粒子具有相同的平均动能(或速度),并且它们在壁上施加相同的力。随着面积的增加,总压力(每单位面积的力)下降。同样,如果温度和摩尔数恒定,体积的减小会导致压力增加。
摩尔数对测试部件压力的影响
当温度和体积保持恒定时,气体摩尔数的增加会增加零件内部的压力。当颗粒对零件壁施加力时,零件内部会产生压力。随着颗粒数(摩尔数)的增加,每单位面积施加的力(压力)也会增加。
考虑压力变化引起的泄漏率
为了正确检测泄漏率,应允许由上述因素引起的压力波动。通常,情况并非如此,在实践中,泄漏测试是在没有适当的填充和稳定时间的情况下进行的。为了解释这些压力变化,需要一个适当的关系来解释压力损失。
推导压力损失与泄漏率的关系
使用理想气体定律,可以推导出合适的关系,允许通过零件中的压力损失来确定泄漏率。泄漏率可以看作是每秒通过零件逸出的气体量。然后可以修改这种关系,以解释压力、温度、体积和摩尔数变化的影响。
根据理想气体定律,测试部件中的摩尔数可以表示为:
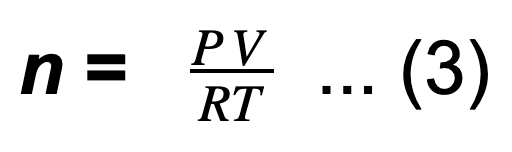
如果
NL = 损失的气体摩尔数
P = P自动取款机 = 气压
V = L.R=每秒逸出的气体泄漏率或体积
则等式 (3) 变为:
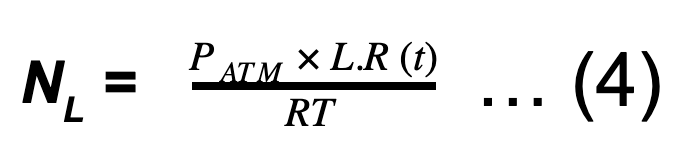
因此,剩余的摩尔数NR将为:
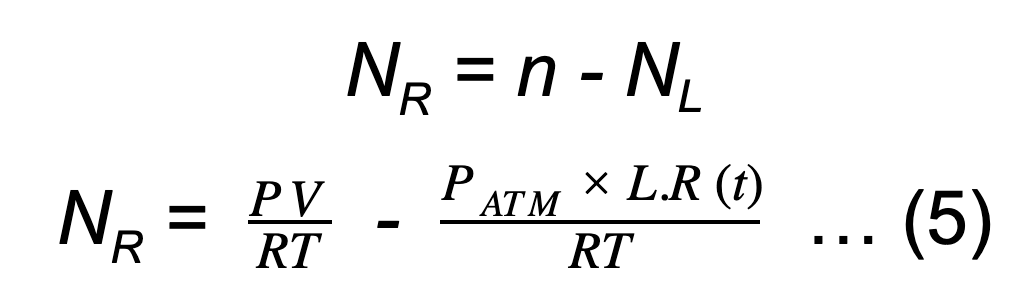
使用理想气体定律,在恒定温度下,时间后的剩余压力(t)可以由下式给出:
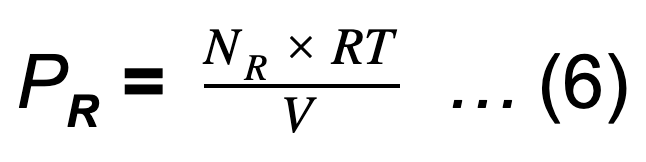
将等式 (5) 中的 N R 值放入等式 (6) 并求解P R,我们得到:
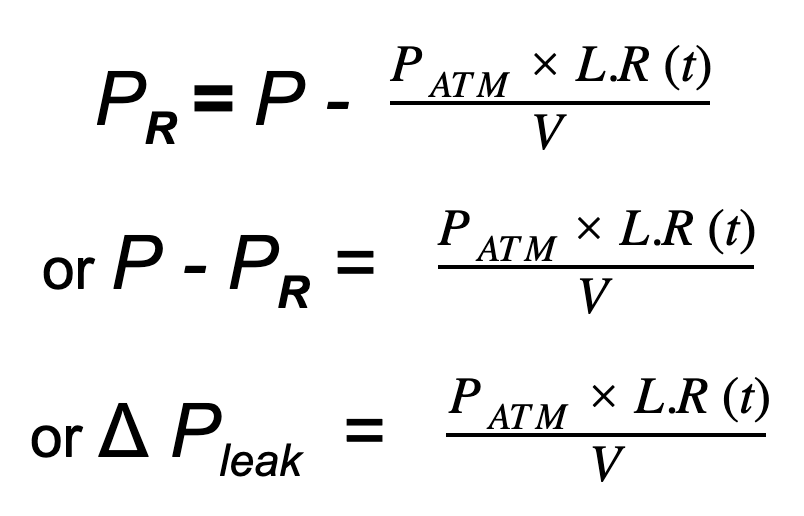
求解泄漏率 (L.R) 产量:
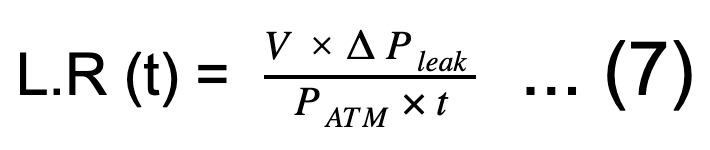
用于适应压力损失的修正方程。公式(7)给出了当测试体积、温度和PATM被视为常数时计算泄漏率的关系。如上所述,实际泄漏率(或压力变化)受体积和/或温度变化的影响。
为了适应这些压力变化,对主部件或“无泄漏部件”进行了测试。尽管没有真正的泄漏,但由于上述原因,该非泄漏部分发生了一些压力变化。这种压力损失称为“零偏移”系数。在考虑“零偏移”因子后,可以修改公式(7)。修改后的公式可用于确定测试部件的泄漏率。从所考虑的测试部件的压力变化中减去无泄漏部分的零偏移系数或压力损失。通过这样做,可以适应由于温度和体积引起的压力变化,并且可以确定正确的泄漏率。修改后的公式为:
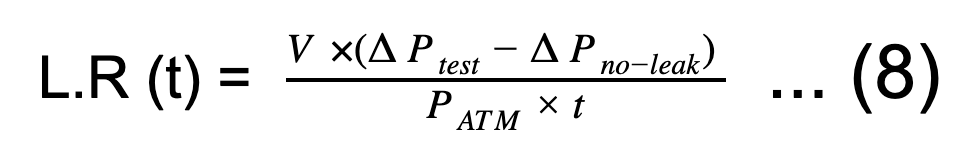
L.R (t)=泄漏率(scc/s)
t=时间(秒)
ΔP test =测试期间测试部件的压力损失 (psi)
ΔP non-leak=无泄漏部分的压力损失 (psi)
V=体积(立方厘米)
过程可重复性
如果ΔP test之间的差异测试和 ΔP non-leak无泄漏不够好,工艺的可重复性会受到影响被测零件的环境因素的影响。测试期间填充和稳定时间的选择将直接影响测试结果。成功结果的最大贡献者将来自填充步骤。具有更多顺应性(体验扩展能力)的部件将需要达到平衡点。在较高的测试压力下,更长的填充步骤将使热力学过程也达到平衡。减少或消除这两个因素将导致ΔP的差异更大,从而改善测试。
